Mittelwert
Wenn ich mit Skripten wie End2End und anderen Werte erfasse, dann ist auch immer ein Mittelwert interessant. Wer ich eine bekannte Datenmenge habe, dann kann ich einfach alle Einzelwerte addieren und durch die Gesamtanzahl der Werte dividieren. Anders sieht es aber aus, wenn ich kontinuierlich Werte bekomme und das Ende nicht abzusehen ist. Ich habe mir dazu eine Verfahren überlegt, wie ich einen "gleitenden Mittelwert" ermittle. Vielleicht gibt es es ja sogar eine mathematische Beschreibung und mein Ansatz mag nicht neu sein, aber da der Code häufiger vorkommt, habe ich ihn hier beschrieben.
Beachten dazu auch End2End Werte
Option1: Arithmetisches Mittel über die letzten Werte
Wenn ich einen Mittelwert der z.B. letzten 10 Werte ermitteln möchte, kann ich mir natürlich einfach die Werte speichern und errechnen. Wann immer ein neuer Wert hinzu kommen, werfe ich den ältesten aus der Liste heraus, addiere den neuen Wert in die Liste und starte die Berechnung erneut. Einfach , verständlich aber vielleicht ineffektiv, weil jedes mal die Summe errechnet wird.

Der Folgewert ermittelt sich dann eben aus den nächsten Werten. Wenn Sie die Formeln anschauen, dann finden Sie aber auch einen kurzen Weg heraus, um aus dem letzten Mittelwert den nächten zu ermitteln.

Allerdings muss man auch dazu sie neben dem Mittelwert auch den ältesten Messwert des vorherigen Mittelwerts merken und da man beim darauffolgenden Schritt dann doch den Wert2 braucht, hat man nicht viel gewonnen.
Option2: Gleitende Berechnung
Aber schaut man sich die Formel genauer an, dann geht in dem Beispiel jeder Wert nur zu 1/5 ein, d.h. können um maximal 20% des aktuellen Mittelwerts abweichen. Klar ist der Wert nicht genau aber mit geht es ja auch nicht um Budget-Rechnungen oder Zählen von Geldstücken sondern die Mitführung eines Mittelwerts, um Abweichungen davon zu bewerten. Und daher habe ich als Vereinfachung statt des ältesten Werts den alten Mittelwert eingesetzt.

Das lässt sich natürlich vereinfachen zu:

Wobei sich die Division noch zusammenfassen lässt und in der PowerShell ein lesbarer Einzeiler draus wird.
$mittelwert = $mittelwert + ($messwert - $mittelwert)/5
Will man die Menge an zusammengefasste Werte ändern, muss nur der Divisor angepasst werden.
Die Abweichung vom arithmetischen Mittelwert wird um so geringer, je mehr Werte in die Ermittlung eingehen. Bei einem Mittelwert über 10 Werte halbiert sich der Einfluss eines einzelnen Werts. für die Abschätzung von Abweichungen sollte das allemal ausreichen.
Gegenüberstellung
Ich bin nun kein theoretischer Mathematiker und meine Studienzeit ist schon einige Jahrzehnte her. Aber ganz auf meine Einschätzung verlassen wollte ich mich nicht. Daher habe ich Excel bemüht um ein paar Werte ermitteln und darstellen zu lassen. Ich habe einfach eine Messreihe aus 20 Werten erstellt und mit dem arithmetisches Mittel über die letzten 5 Wert als auch meine eigene "Formel" eines gleitenden Mittelwerts über 5 und 10 Werte erstellt.
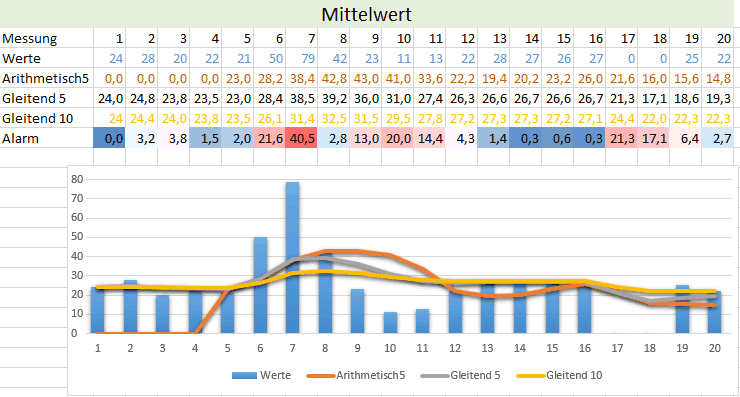
Es ist natürlich klar, dass mit unterschiedlichen Formeln auch unterschiedliche Linien entstehen. Ich habe hier auch absichtlich mal einen "Ausschlag" nach oben (Wert 7) und zwei ausgefallene Werte als "Null"-Werte (17/18) eingebaut um die Auswirkungen zu sehen. Das arithmetische Mittel über die letzten 5 Werte scheint aber sogar stärker zu schwanken als mein gleitender Mittelwert. Das kann natürlich auf diese Testdaten bezogen sein. Aber die Abweichungen sind nach meiner Einschätzung minimal und der gleitende Mittelwert ausreichend, um bei Messungen zumindest Ausschläge zu erkennen.
Dazu habe ich in der Zeile "Alarm" einfach die absolute Abweichung des Messwerts vom Mittelwert errechnet und farblich codiert. Zumindest in diesem Beispiel werden Abweichungen ausreichend zuverlässig erkannt und der gleitende Mittelwert hat sogar eine weniger große Amplitude als das arithmetische Mittel. Wenn die Messstelle also idealerweise konstant bleibt, dann scheint der gleitende Mittelwert sogar Vorteile zu haben. Wenn ich aber eine Messstelle auswerte, die sich auch gewollt verändert (z.B. die Temperaturkurve einer Heizung, der Sonnenstand o.ä., dann sollte ich die Alarmschwelle etwas höher setzen.
Sonderfälle
Es gibt aus meiner praktischen Betrachtung zwei Fälle die gesondert betrachtet werden müssen.
- Erster Messwert
Der Code muss natürlich eine Lösung bieten, den ersten Messwert zu verarbeiten, wenn es keinen alten Mittelwert gibt. Ich habe mir dabei geholfen, dass ich den ersten Messwert einfach als ersten Mittelwert nutze und erst nach einigen Messungen dann eine höhere "Empfindlichkeit" - Negative Werte durch
Rollover
Es gibt Werte (z.B. Anzahl der Pakete einer Netzwerkschnittelle) die inkrementelle Werte sind und durch eine Differenz zum vorherigen Wert erst den richtigen Wert liefern. Findet hier ein Rollover statt, dann kann der Wert "negativ" sein. Diese Messung ignoriere ich einfach, indem ich den aktuellen Mittelwert als Messwert einfüge und hoffen, dass der nächste Wert dann wieder passt.
Praktischer Einsatz
Den dazugehörigen Code habe ich in verschiedenen Projekten genutzt, z.B.:
- Messagetracking/Queues
Hier interessiert mit das durchschnittliche Mailvolumen und Mailgröße innerhalb eines vorgegebenen Fensters um Ausschläge noch oben oder unten zu erkennen. - Queues
Auch Warteschlangen lassen sich damit gut überwachen und je Warteschlage einen ""Regelwert" nutzen ohne manuell diesen vorgehen zu müssen. - Netzwerklast
Erfasst man vom Router oder Netzwerkkarte die Anzahl der Pakete oder Bytes pro Zeiteinheit, ist auch hier ein Mittelwert ein guter Anhaltspunkt um große Abweichungen außerhalb der "Norm" zu ermitteln - End2End Monitoring
Aktuell ist z.B. im Skript End2End-File der Code hinterlegt, um die Zeit für Zugriffe auf eine Datei auf einem Share zu mitteln und größere Abweichungen zu erkennen und zu melden. - Transactionlogs/Zeit
Exchange CCR und DAG-Systeme schreiben Transactionslogs und wenn kein Circular Logging aktiv ist, dann nehmen die einfach immer zu. Hier sind absolute Werte natürlich wichtig aber gerade das Wachstum pro Zeiteinheit erlauben viel früher schon eine Alarmierung.
Es gibt noch sehr viel mehr Einsatzort für einen Mittelwert
Codeauszug
Folgender Teilcode soll zeigen, wie einfach ein gleitender Mittelwert umgesetzt werden kann.
# Iitialisierung
[int]$mittelwert = 0
#ab hier ist dann die Messschleife
while ($true) {
# Messwert ermitteln
$performance = get-counter ......
# Sonderfaelle abfangen
if ($mittelwert -eq 0 ) {
$mittelwert = $performance # First run
}
elseif ($performance -lt 0) {
# skip the midnight rollover
}
else {
if ($performance - $mittelwert -gt $Alarmdelta) {
write-host "ALARM: exceeded limit `r`n"
}
$mittelwert = $mittelwert + ($performance - $mittelwert)/5
}
}
Der Aufwand ist also minimal um mit gleitenden Mittelwerten zu arbeiten.














